RSCH FPX 7864 Assessment 1 Sample FREE DOWNLOAD
RSCH FPX 7864 Assessment 1
Descriptive Statistics
Student name
Capella University
RSCH-FPX7864
Professor Name
Submission Date
Descriptive Statistics
Part 1: Histogram
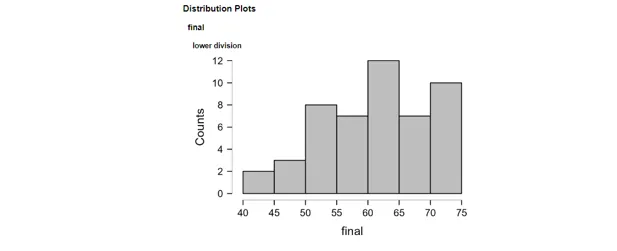
Lower Division
The histogram displayed above gives the frequency distribution of final examination scores of lower-division students. The various intervals of the scores help in assessing the academic performance of the students in the course. The variables analyzed in the histogram include finals and lower division classes, in which final examinations are the independent variables and lower division classes are the dependent variables. The histogram shows the distribution of student scores within the 40 to 75 score range with intervals of 5. The frequency distribution was used to assess the number of students who had attained specific score ranges through the histogram. The largest frequency in the histogram was 60-65 ,with 12 out of 49 students who fell into that range. The analysis of the histogram displayed left-skewed data features as more scores were concentrated in the left part (Chattamvelli and Shanmugam, 2023). Furthermore, the analysis confirmed the skewness to the left as it identified a long tail to the left relative to the right.
Upper Division
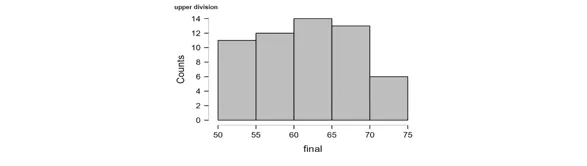
The histogram area represents the number of times the student scores in an upper division occurred. The intervals of the scores help to determine the levels of student achievement. The variables represented in the histogram are the final and upper division classifications with final being the independent variable and upper division serving as the dependent variable. The histogram shows the distribution of scores in the range of 50 to 75 with 5 5-point interval. Through the frequency distribution of the histogram, it is possible to calculate the number of students who reach a score within a range of specific levels. There were 14 students in the range of 60-65, making up the maximum frequency distribution in the histogram out of 56 total students. The histogram was symmetrical, indicating the data was evenly distributed on both sides, and bell-shaped, as revealed by a frequency distribution analysis. The uniform bell-shaped shape of the histogram also confirmed the normal distribution nature present in the data.
Part 2: Descriptive Statistics
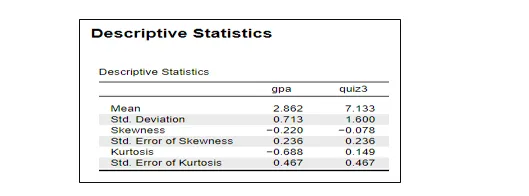
A small difference between the mean and standard deviation indicates fewer data variations, and a large difference indicates more data variation. The descriptive analysis includes the measures of mean, skewness, kurtosis, and standard deviation that help to determine the centrality and normality attributes of the data (Pinsky and Klawansky, 2023).
In the case of GPA, the mathematical values of mean and standard deviation are M= 2.862 and SD= 0.713. By using means plus standard deviation (2.862+0.713=3.575) to calculate the maximum value of GPA data, one can show limited scatter and improved central tendency. In Quiz 3, analysis showed that the mean and standard deviation values were M=7.133 and SD=1.600. The maximum calculated mean of the data used in Quiz 3 is: (7.133 + 1.600 = 8.733), indicating limited dispersion and more data centrality.
In the case of the GPA variable, the skew and kurtosis were -0.220 and -0.688, respectively. The value was not exceeding acceptable normal limits (-2 to +2), hence normal data distribution (Chattamvelli and Shanmugam, 2023). Concerning the Quiz 3 variable, the skew and kurtosis of 0.078 and 0.149 were also within the desirable range of normality (-1 to +1) and far below the acceptable range (-2 to +2) about psychometrics. The descriptive statistical interpretation indicated that the skewness and kurtosis values of the variables are within the optimal -1 to +1 range, and both the skewness and kurtosis values validate that the data distributions are both excellent normal.
Conclusion
The histogram showed the academic scores of both upper and lower division students. Student achievement levels were measured using the frequency distribution of scores through the histogram. However, measures of central tendency and variability of the data will be determined by use of descriptive statistics. Also, skewness and kurtosis values will be used to confirm the normality properties of the data. As per the descriptive analysis, following data distribution patterns were observed with GPA and Quiz 3 variables: normal.
Are you struggling with RSCH FPX 7864 Assessment 3? Get expert guidance on t-test application, clear examples, and step-by-step support today!
Step-By-Step Instructions To Write RSCH FPX 7864 Assessment 1
Follow the step-by-step instructions given below to complete your RSCH-FPX 7864 Assessment 1
Objective:
Analyze and interpret histograms and descriptive statistics in a short academic report.
Step 1: Examine the data:
- Look closely at two histograms (like grades for lower and upper divisions) and one table of descriptive statistics (like GPA and Quiz 3).
- You need to know what the data is before you can understand it.
Step 2: Discuss each histogram:
- For each histogram, write a paragraph that answers this question:
- What is a histogram? “Distribution of final grades for upper division students” is one example.
- What does it look like? Check out the shape (parallel, left/right skewed), the mode (the range of the most common values), and how the data is spread out.
- What does it mean? In a few words, tell us what the shape means for how well the group did. For instance, “The right skew means that most students did worse than average.”
- This means you can write about visual data.
Step 3: Interpret descriptive statistics:
For each variable, like GPA or Quiz 3, write a paragraph that explains the following:
- The center’s average score (mean).
- Change: The standard deviation (if the scores are close to the mean or spread out).
- To find the peak values, use kurtosis, and to find the symmetry, use skewness. Please tell me if the numbers are “normal” (between -2 and +2).
- Visit the Capella Writing Center for help with writing.
Step 4: Write a brief conclusion:
Action: Summarize the main results of the histograms and statistics in 1–2 paragraphs.
Reason: This deepens your analysis and provides a compelling conclusion.
Step 5: Format according to APA 7th edition:
Action: Include a title page and a bibliography with at least 2–3 scholarly sources (e.g., a statistics textbook or a peer-reviewed article that explains the skewness).
Reason: Proper formatting and citations are essential for academic credibility.
Easy Writing Guide: IEC Paragraph Method
Use this simple structure for each statistic you are explaining:
- Introduction: State the fact. (“The skewness for GPA is -0.220”)
- Explain: Define the term. (“Measures the imbalance in the dataset.”)
- Conclusion: Interpret the value and cite the source. (“This negative value indicates a left-skewed distribution, meaning most values are high (Chatham Valley & Shanmugam, 2023).”)
Support Platforms
Statistical Help: Capella Library (search for “Detailed Statistics”).
Writing/APA: Capella Writing Center.
Final Checklist
- Both histograms have a shape, a center, and a spread.
- I checked all the numbers, including the mean, SD, skewness, and kurtosis.
- Used academic sources to explain.
- The conclusion was included.
- There is a list of sources and a title page in APA style.
- Search for errors.
References For RSCH FPX 7864 Assessment 1
You can use the references for your assessment:
Chattamvelli, R., & Shanmugam, R. (2023). Skewness. Synthesis lectures on mathematics and statistics, 91–110. https://doi.org/10.1007/978-3-031-32330-0_4
Jideani, V. A., Jideani, A. I. O., Zheleva, I., Todorov, T., Bozkurt, H., Göğüş, F., Schleining, G., Horváth, Z. H., Hodúr, C., Suwannaporn, P., Brandão, T., Quintas, M., Silva, C., & Muntean, E. (2024). Basic statistics for data collection and treatment. Springer EBooks, 1–154. https://doi.org/10.1007/978-3-031-51568-2_1
Pinsky, E., & Klawansky, S. (2023). MAD (about median) vs. quantile-based alternatives for classical standard deviation, skewness, and kurtosis. Frontiers in Applied Mathematics and Statistics, 9, e1206537. https://doi.org/10.3389/fams.2023.1206537
Best Professors To Choose From For 7864 Class
- Dr. Brock Boudreau
- Dr. Scott Wowra
- Dr. Lynda Cable
- Dr. Art Bangert
- Prof. Raphael
(FAQs) related to RSCH FPX 7864 Assessment 1
Question 1: How do I read histograms for the first RSCH-FPX 7864 test?
Answer 1: At Tutors Academy, we assess someone’s performance by considering several key criteria. These include their score ranges, frequencies, and the shape of the distribution.
Question 2: What do skewness and kurtosis mean when you talk about descriptive statistics?
Answer 2: According to Tutors Academy, skewness refers to the degree to which data leans to the left or right. And kurtosis is how sharp or flat a curve is.
Question 3: How can I determine if the test data is normally distributed?
Answer 3: At Tutors Academy, data is considered normal when the skewness and kurtosis values fall between -2 and +2.
Do you need a tutor to help with this paper for you with in 24 hours.
- 0% Plagiarised
- 0% AI
- Distinguish grades guarantee
- 24 hour delivery