
RSCH FPX 7864 Assessment 1 Descriptive Statistics
Looking for support with RSCH FPX 7864 Assessment 1 Descriptive Statistics? Our team of experts is available to assist you. Just enter your email, and our expert will contact you within 2 minutes.
Statistical description is one of the most important approaches to nursing research and practice, giving nurses the means to examine and comprehend healthcare data carefully. The nurses can achieve accomplished demographics via descriptive statistics in which the healthcare data can be summarized for clinical characteristics and patient outcomes, thus, evidence-based decision-making can be enabled and enhance patient care. The measures of central tendency giving an idea of an average age of patients or a median length of hospital stay are what a healthcare provider often tend to look out for because they help to learn more about the typical experience in a healthcare setting (Polit, & Beck, 2021). Moreover, for those nurses who are seeking to assess the dispersion measures on vital signs they can resort to standard deviation or on medication dosages, they can rely on range. Charting frequencies and graphs are remarkable in nursing as they allow for the visual presentation of trends and patterns of data. Histograms, pie charts, and bar graphs are helpful in understanding where improvisations as well as how focused intervention can be pursued.
Histograms for Lower Division Students and Upper Division Students
-
Part 1:
-
Lower Division:
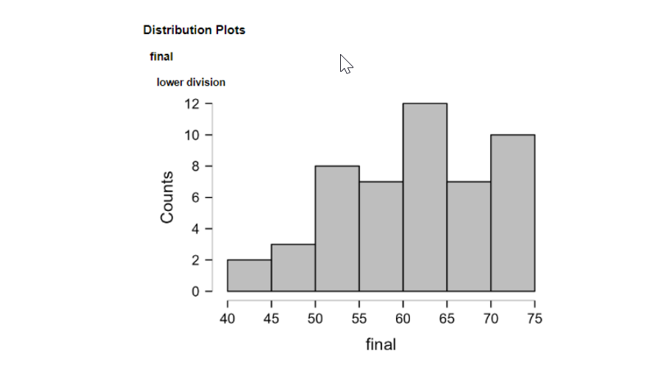
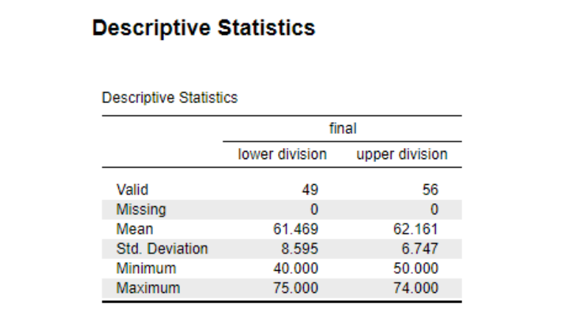
The graph lists the scores of the students in the final exams. The base line of the histogram indicates the score of 49 students. The independent variable is the final exam score, and the low-level division is the dependent variable in the histogram. The interval for final exam scores is 40-75. For simple output analysis, final exam score had a gap of 5 items whereby 40-45 and 60-65. Of the 49 scholars, two individuals scored between 40 and 45. Three students made 45-50 marks, and the eighth student was from 0- 55. The number of students whose scores falls into the various ranges as from 55 – 60 is seven whereas 12 are in the range 60-65. However, only seven and ten students scored between 65 -70 and 70 – 75 respectively. The majority of the scores of the students are clustered in the range of 60-65. The histogram shows that there is a left-skewn distribution pattern because most values are at the left side (Pajankar, 2021). The market value has a span of 40.000 to 75.000. For the lower division’s mean values are M=61.469, and the standard deviation becomes SD=8.595. The median indeed is more than the mean. This clarifies that the data underlying the histogram has left skewness.
-
Upper Division:
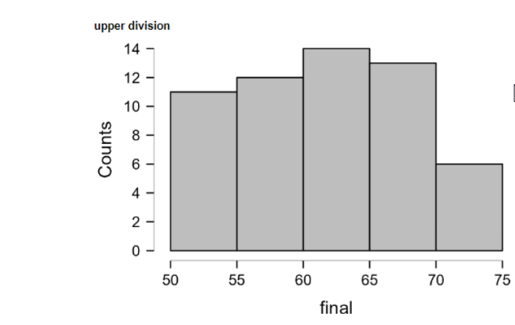
Histogram enables us to obtain statistics of the scores students have scored in their final exams. The class scores obtained from the 56 students are shown in the upper part of the histogram in the graph. The ultimate assessment (the exam score) is the independent variable and the lower collegiate year is the dependent value in the histogram. The spectrum of the final exam grades is spans from 50 to 75. To make the histogram a little easier to interpret, we placed the gap of five numbers, e.g. 50-55 and 60-70. However from the fifty-six students, only several eleven students got a 50-55 score. The grade breakdown is as follows: twelve students get 55 to 60; the other fourteen belong to the range of 60 to 65. One of students who got average score 65-70 was 13, and the student who scored about 70-75 was 6. Generally, student scores are closer to range of 60-65. The histogram is the fact that the data record has been made. Observation is that as the mode can be defined as the value where the greatest mass or frequency is concentrated, the mode is always a normal distribution which is characterized by a bell-shaped curve. Almost all data lies close to the middle and will decrease as farther as it goes from the center, so the data are equally distributed near the center. For the lower division, the statistics show the mean values as M=62.161, and the standard deviation is SD=6.747. The close to mean value is behind the mean which means that our data is normally distributed (Pajankar, 2021). From 50.000 and 75.000, the given range of the value is spanned.

Data Set Interpretation
-
Part 2:
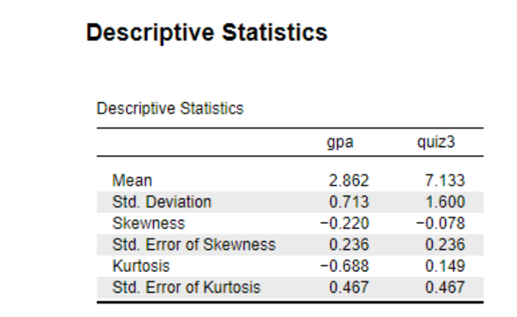
This data set also offers information about the students’ performance using GPA and quiz 3 scores. These scores are analyzed with descriptive data. Diverse variables that are, mean, standard deviation, skewness, and kurtosis, can be obtained through descriptive analysis. The average is the mean, and the deviation from that average is illustrated by the standard deviation.(Darling, 2022). The mean and the SD of GPA are M=2.862 and SD=0.713, correspondingly. Furthermore, the value of skewness and kurtosis are respectively -0.220 and -0.688. If the data symmetry has a negative skewness value this means the distribution has a higher peak value on the left-side tail of the histogram (Berger & Kiefer, 2021). On the other hand, the absence of kurtosis indicates that there is no uniformity in the data distribution. The mean and standard deviation for Quiz 3 would be 7.133±1.600. Additionally, the kurtosis is 0.149 while the skewness is -0.078.A negative sign in the skew test reveals that there is an evident left skew in this dataset. On the other hand, Quiz 3 Kurtosis value suggests almost normal distribution of data. Descriptive statistics present thorough data on the degree of the skewness and flatness that will determine whether or not the data is normally distributed. Values range from -1 to 1, -2, and +2 are in the acceptable zone while 1 is the ideal situation. In contrast, the ones that are outside the range of -3 or +3 can be interpreted as though they are abnormal.
RSCH FPX 7864 Assessment 1 Descriptive Statistics Data Set Interpretation
Skewness and Kurtosis:
The values that decide normal distribution are skewness and kurtosis are measures of data normality. The skewness value indicates where the data is more concentrated on the two sides of the bell curve to determine the symmetry or asymmetry of the data set. Data distribution may be balanced, skewed positively, skewed negatively, or have zero skewness (Hatem et al., 2022). A positive skewed dataset is portrayed where a mean value is greater than the median value and the shape of the distribution has a tendency to be on the right of the curve. On the flipside of positive skewness, there is negative skewness which comes with a distribution that tends to be left-skewed than right in the distribution, plus a mean that is lower than the median. Skewness zero refers the case when the median and mean are indistinguishable. Descriptive analysis gives the kurtosis and skewness values to tell the data distribution of GPA and Quiz3. Additionally, the calculated skewness for GPA is -0.220 and -0.078 for the Quiz 3. The GPA skewness is negative, that means data distribution is in front of average position. On the other hand; though, the case of the skewness standard error of 0.236 is presented. Besides, our standard deviation remains to be 0.713 and the mean 2.862. The result Skewness value of -0.220 for GPA demonstrates that the normality of data is validated, since it falls within the range (-1 to +1). In addition, the negatively-skewed Quiz 3 number of -0.078 is still within the normal range of this value indicating a predominantly positive image of the campaign. The distribution of data is also an optimal one because it is evident from the value of the parameter.
Kurtosis:
The kurtosis statistic is appropriate for indicating whether data distribution has many tails or the few. This value serves as the measure of how heavy-tailed and flat the distribution is of data compared to the normal distribution (Hatem et al., 2022). Kurtosis can be zero (mesokurtic), positive (leptokurtic), and could be negative (platykurtic). In a regular bell-shaped distribution, the value of zero is 3. On the other hand, the power a positive kurtosis has against normal distribution is more pronounced in the sense that it has larger peaks, heavier tails, and a value greater than 3. When compared with a normal distribution, a negative kurtosis distribution differs from a normal one in a sense that its peaks are flatter and its tails are thinner and it is equal to 3. The kurtosis data types will be more about the distribution of the dataset. The kurtosis coefficient for the GPA variable is -0.688 and the standard error determined is 0.467. -2 to +2 number includes this number into the valid range. The kurtosis and the standard of error for the test 3 variable appear as 0.149 and 0.467. The sought kurtosis places in normality range, -2 to +2, as well. The skewness value for the GPA variable is -0.220 and that of the kurtosis is -0.688, but both of them fall within (-1 to +1) which is the ideal range of normalcy, indicating that the data follows a normal distribution. The calculated kurtosis (-2 to +2) and skewness (-0.078) for the variable quiz 3 are in within the acceptable norm range.
To explore more related samples click below:
NURS FPX 9901 Nursing Doctoral Project 1
Conclusion
Descriptive statistic utilization is a process that is a precondition in nurse research and practice. It is a tool that provides the healthcare professionals with a solid set of means to analyze and perceive health data correctly. By utilization of the statistical representation data sets can be transformed into meaningful clinical patterns that can be used for evidence-based decision-making and improving patient care. Measures of central tendency like mean and mean are invaluable for understanding of the most common patients’ features. Scores of dispersion, like standard deviations, are what quantifies variations within the data. For instance, showing a histogram or a graph may prompt an observer to spot a trend and an effective solution to a healthcare management problem. An example can be in the course of analyzing sample data which descriptive statistics help in giving very critical insight in regard to student performance, as in the case of final exam results and GPA. The histograms demonstrate that the students of lower levels were showing a left-skewed distribution with the mean score around 60-65 while the upper level students was exhibiting even distribution pattern with around the same range. Furthermore, descriptive statistics, from skewness to kurtosis as measures of data distribution flatness and symmetry, give notations that enhance our comprehension of data further. The descriptive statistics represent the necessary devises in the nursing research and practice, since they empower nurses to process complex datasets and make evidence-based decisions to enhance the quality of patient care.
References
Flegal, J. M. (2021). Data visualization: Charts, maps, and interactive graphics. robert grant. The American Statistician, 75(1), 113–113.
https://doi.org/10.1080/00031305.2020.1865062
Razak, N. A. S. A., Habib, S., Shukor, M. Y. A., Alias, S. A., Smykla, J., & Yasid, N. A. (2024, January 4). Isolation and characterisation of polypropylene microplastic-utilising bacterium from the antarctic soil. ArXiv.org.
https://doi.org/10.48550/arXiv.2401.02096
Wolf, Z. R. (2024, March 1). Expert-Type content validity applications to doctor of nursing practice projects. | journal of doctoral nursing practice | ebscohost. Openurl.ebsco.com.
Are you in need of help with RSCH FPX 7864 Assessment 1 Descriptive Statistics? Our experts are ready to assist you. Simply provide your email, and our expert will reach out to you within 2 minutes.
