
- RSCH FPX 7864 Assessment 3 t-Test Application.
Data Analysis Plan
The factors utilized for the t-test and Levene’s test in the RSCH FPX 7864 Assessment 3 t-test Application were conclusive and reviewed. The final part shows the number of correct responses on the previous preliminary of the year, while the audit variable is described as the students who attended the review meetings, indicated by 1 = no and 2 = yes. The review is considered a two-level fixed factor, but the latter is treated as exploratory for this overview.
Online Meeting Attendance Impact
The audit question is, does the get-together of understudies who attended the outline meeting (yes)? Additionally, the party of understudies who didn’t (no) have commonly extraordinary mean grades on the Last, most colossal test? The Invalid speculation is that the mean grades of the understudies who went to the online meeting and those who didn’t appear for the social affair don’t separate endlessly from each other. Finally, the substitute speculation is that understudies who went to the outline meeting and understudies who didn’t have a gigantic separation of psyche on the previous test.
Testing Assumptions
Using Levene’s test, a t-test overviews the assumption of indistinguishable changes between two social events (Kim, 2015). The variable “last” in the result was introduced to Levene’s test to pick on the off chance of a tantamount instability between the two parties (people who went to concentrate on social occasions and those who didn’t). There are df1=1, levels of possibility (df1, df2), and a test assessment (F) of 0.740. The p-worth of the test is more essential than 0.392, with the standard alpha edge of 0.05. The invalid speculation, which implies that the instabilities of the two social affairs are the Same, is suitably not pardoned. Put shockingly, the results of the Levene test don’t reveal a break in the homogeneity of differentiations premise. Consequently, the homogeneity of changes expected by the t-test is fulfilled, and the qualifications of the two parties are the same.

Using Levene’s test, a t-test overviews the assumption of indistinguishable changes between two social events (Kim, 2015). The variable “last” in the result was introduced to Levene’s test to pick on the off chance of a tantamount instability between the two parties (people who went to concentrate on social occasions and those who didn’t). There are df1=1, levels of possibility (df1, df2), and a test assessment (F) of 0.740. The p-worth of the test is more essential than 0.392, with the standard alpha edge of 0.05. The invalid speculation, which implies that the instabilities of the two social affairs are the Same, is suitably not pardoned. Put shockingly, the results of the Levene test don’t reveal a break in the homogeneity of differentiations premise. Consequently, the homogeneity of changes expected by the t-test is fulfilled, and the qualifications of the two parties are the same.

Descriptives
T-Test Results and Analysis
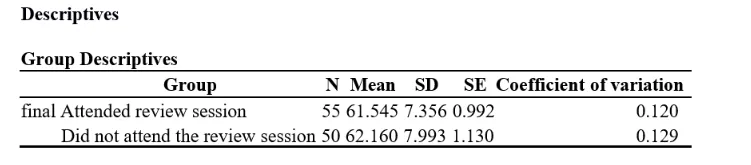
Each party’s means and standard deviations are as indicated by the following:
- Part pack at the review meeting: m= 61.545, sd = 7.356
- Didn’t go to the get-together audit meeting: sd = 7.993, m = 62.160
The free model’s t-test was utilized to determine whether there was an enormous contrast between the systems for the two social gatherings.
The results of the t-test are as follows:
- t = – 0.410
- df = 103
- p = 0.682
Since there is a deficiency regarding affirmation, the invalid speculation can’t be pardoned, as shown by the p-worth of 0.682, which is more fundamental than the standard alpha limitation of 0.05.
In this manner, we reason that there is no statistically monstrous capability in the last test. Scores between understudies who participated in the survey of social affairs and those who didn’t. We can’t pardon the invalid speculation thinking about statistical results, and the elective theory isn’t mainly kept up with.
Statistical Conclusions
The defense behind this audit was to close whether the last preliminary of the year scores of understudies who went to outline social events and individuals who didn’t vary statistically basically. A free model t-test was utilized to embrace the assumption of practically identical differences, and the results were perfect. The assessment observed no statistically tremendous capability between the two parties’ mean last grades. Along these lines, there is no attestation to help the speculation that concentrating on social events would refresh test execution, and the invalid theory was not delineated.
RSCH FPX 7864 Assessment 3 t-Test Application
The free model t-test can be utilized to audit up to two social events promptly. The t-test should be used with a solitary free and subordinate variable; it doesn’t ponder different evaluations. One more burden of the t-test is that it could show remaining part impacts, which initiates that, as opposed to including pack contrasts, it could highlight issues with emphasized assessments. Different factors, similar to earlier scholarly execution or study affinities, may impact the results yet were not considered during the review. Likewise, there may be extra explanations for the results. For instance, it’s conceivable that the audit get-togethers went insufficiently or that understudies didn’t go as often as possible enough to impact their grades.
Application
In applied lead analysis (ABA), the reasonableness of two certain mending meditations for the association of a specific direct issue in people with manufactured disproportion or other formative obstacles can be measured by being measured using the free model’s t-test. Lead experts utilize free models t-test applications in the field of ABA for the following reasons. The plans and intercessions for understudies’ solid way of acting remarkably rely on the results of t-tests for subordinate components. Each part in this particular social gathering of understudies is surveyed two times on a result variable, for example, the pretest-posttest plan, which is the critical application of the t-test in treating them.
By looking at the mean changes in the dependent variable between treatment groups in the RSCH FPX 7864 Assessment 3 t-Test Application, I could conclude that the intervention was more effective in reducing the assigned behavioral issue. Using this data, clinical providers, researchers, social workers, and caregivers could find it easier to select the most effective intervention options for their patients or loved ones. Explore our assessment RSCH FPX 7864 Assessment 1 for more information.
References
Capella University (n.d.) 7864 Course Study Guide. Kim, T. K. (2015). T test as a parametric statistic. Korean Journal of Anesthesiology, 68(6), 540. https://doi.org/10.4097/kjae.2015.68.6.540
